无脑循环爆破法

import java.lang.management.ManagementFactory;
import java.lang.management.ThreadMXBean;

/**
 * PrimeNumber
 * 博客地址www.xysycx.cn
 *
 * @author xysycx
 * @version 1.0
 * 2019/10/29 下午11:14
 * //素数，指在大于1的自然数中，除了1和该数自身外，无法被其他自然数整除的数（也可定义为只有1与该数本身两个正因数的数）。
 *     // 大于1的自然数若不是素数，则称之为合数（也称为合成数）。例如，5是个素数，因为其正约数只有1与5。
 *     // 而6则是个合数，因为除了1与6外，2与3也是其正约数。
 *     // 算术基本定理确立了素数于数论里的核心地位：任何大于1的整数均可被表示成一串唯一素数之乘积。
 *     // 为了确保该定理的唯一性，1被定义为不是素数，因为在因式分解中可以有任意多个1（如3、1×3、1×1×3等都是3的有效约数分解）
 **/
/*试除法*/

public class PrimeNumber {
    private static final ThreadMXBean mxBean = ManagementFactory.getThreadMXBean();
    public static void main(String[] args) {
        int num;
        int j=2;
        System.out.println(1);
        for (int i = 2; i <=1000000 ; i++) {
            for ( j = 2; j<=i ; j++) {
                num=i%j;
                if (num==0){
                    break;
                }
            }
            if (i==j){
                System.out.println(i);
            }
            long sum=mxBean.getCurrentThreadCpuTime()/1000000;

            System.out.println("CPU执行耗时"+sum+"毫秒");
        }
    }
}

一百万范围内用时

埃拉托斯特尼筛法

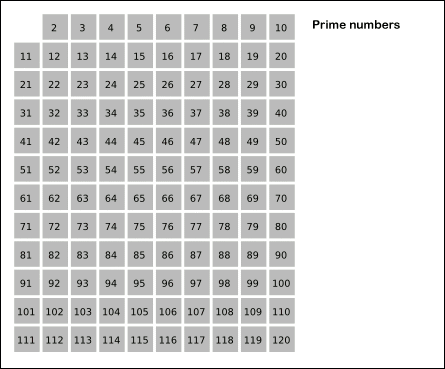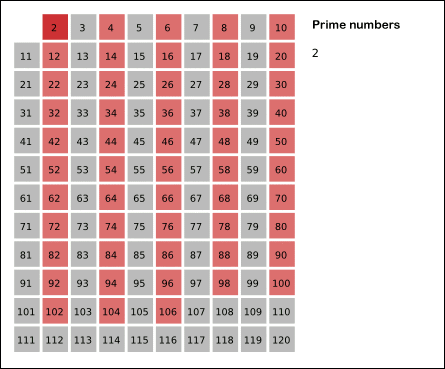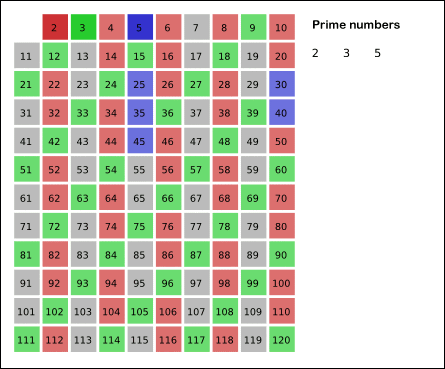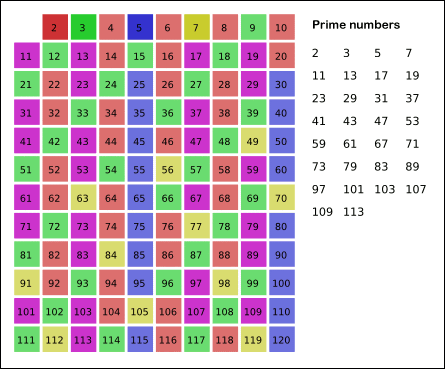
原理是从 2 开始，将每个素数的各个倍数，标记成合数。一个素数的各个倍数，是一个差为此素数本身的等差数列。此为这个筛法和试除法不同的关键之处，后者是以素数来测试每个待测数能否被整除。

import java.lang.management.ManagementFactory;
import java.lang.management.ThreadMXBean;
import java.util.ArrayList;


/**
 * SieveofEratosthenes
 * 博客地址www.xysycx.cn
 *
 * @author xysycx
 * @version 1.0
 * 2019/10/29 下午11:47
 **/
public class SieveofEratosthenes {
    private static final ThreadMXBean mxBean = ManagementFactory.getThreadMXBean();
    public static void main(String[] args) {
        int n = 1000000;//需要筛选的素数的范围 当前是求一百万以内的素数
        int index = 0;
        ArrayList<Integer> numArray = new ArrayList<Integer>(n);

        for (Integer i = 1; i <= n; i++) {//1.从1到n插入集合
            numArray.add(i);
        }


        double psr = Math.sqrt(n);//2.求出n的算数平方根
        System.out.println(n+"的算数平方根为"+psr);
        int num1;
        int j = 2;
        for (int i = 2; i <= psr; i++) {
            for (j = 2; j <= i; j++) {
                num1 = i % j;
                if (num1 == 0) {
                    break;
                }
            }
            if (i == j) {
                System.out.println(n+"的算数平方根以内的素数为"+i);
                for (int k = 0; k <numArray.size(); k++) {
                    if (numArray.get(k)%i==0&&numArray.get(k)/i>1){
                        numArray.remove(k);     //将n平方根范围内的素数的倍数全部从集合中移除
                    }
                }
            }
        }
        numArray.remove(0);//素数修正 1不是素数 从集合中移除
        long sum=mxBean.getCurrentThreadCpuTime()/1000000;//获取当前线程执行耗时 并转化为毫秒
        for(int i = 0 ;i < numArray.size() ; i++){ //遍历集合内素数
            System.out.println(numArray.get(i));
        }
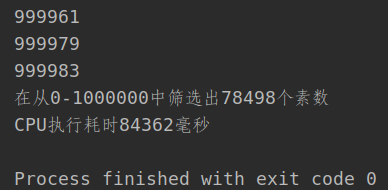
        System.out.println("在从0-"+n+"中筛选出"+numArray.size()+"个素数");

        System.out.println("CPU执行耗时"+sum+"毫秒");
        }
    }